The Landau criterion for Superfluidity
Pascal Szriftgiser1 and Edgardo S. Cheb-Terrab2
(1) Laboratoire PhLAM, UMR CNRS 8523, Université Lille 1, F-59655, France
(2) Maplesoft, Canada
A Bose-Einstein Condensate (BEC) is a medium constituted by identical bosonic particles at very low temperature that all share the same quantum wave function. Let's consider an impurity of mass M, moving inside a BEC, its interaction with the condensate being weak. At some point the impurity might create an excitation of energy and momentum . We assume that this excitation is well described by Bogoliubov's equations for small perturbations around the stationary solutions of the field equations for the system. In that case, the Landau criterion for superfluidity states that if the impurity velocity is lower than a critical velocity (equal to the BEC sound velocity), no excitation can be created (or destroyed) by the impurity. Otherwise, it would violate conservation of energy and momentum. So that, if < the impurity will move within the condensate without dissipation or momentum exchange, the condensate is superfluid (Phys. Rev. Lett. 85, 483 (2000)). Note: low temperature liquid 4He is a well known example of superfluid that can, for instance, flow through narrow capillaries with no dissipation. However, for superfluid helium, the critical velocity is lower than the sound velocity. This is explained by the fact that liquid 4He is a strongly interacting medium. We are here rather considering the case of weakly interacting cold atomic gases.
Landau criterion for superfluidity
Background: For a BEC close to its ground state (at temperature T = 0 K), its excitations are well described by small perturbations around the stationary state of the BEC. The energy of an excitation is then given by the Bogoliubov dispersion relation (derived previously in Mapleprimes "Quantum Mechanics using computer algebra II").
where G is the atom-atom interaction constant, n is the density of particles, m is the mass of the condensed particles, k is the wave-vector of the excitations and their pulsation (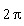 time the frequency). Typically, there are two possible types of excitations, depending on the wave-vector :
In the limit: , with , this relation is linear in and is typical of a massless quasi-particle, i.e. a phonon excitation.
In the limit: , which is the dispersion relation of a free particle of mass i.e. one single atom of the BEC.
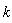Problem: An impurity of mass 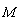moves with velocity 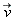within such a condensate and creates an excitation with wave-vector 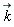. After the interaction process, the impurity is scattered with velocity .
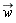a) Departing from Bogoliubov's dispersion relation, plus energy and momentum conservation, show that, in order to create an excitation, the impurity must move with an initial velocity
When , no excitation can be created and the impurity moves through the medium without dissipation, as if the viscosity is 0, characterizing a superfluid. This is the Landau criterion for superfluidity.
b) Show that when the atom-atom interaction constant 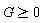(repulsive interactions), this value is equal to the group velocity of the excitation (speed of sound in a condensate).
Solution
References
[1] Suppression and enhancement of impurity scattering in a Bose-Einstein condensate
[2] Superfluidity versus Bose-Einstein condensation [3] Bose–Einstein condensate (wiki)
[4] Dispersion relations (wiki)
