
Maple 2018 continues to push the frontiers of differential equation solving, with new methods that enable Maple to find closed-form solutions to new classes of problems. What follows below describes the novelties in solving nonlinear Ordinary Differential Equations of second order, as well as the new differential elimination package DifferentialThomas. For partial differential equations with boundary condition (PDE and BC), see the corresponding What’s New in Partial Differential Equations.
Maple is the uncontested leader for computing symbolic solutions to differential equations, and Maple 2018 extends its lead in computing closed-form solutions by adding even more classes of problems that can be handled. The four new ODE classes solvable in this release do not admit point symmetries. The method used is based on the S-function method and a generalization of it to classes of equations with infinitely many members.
Examples
To display special functions using textbook notation, use extended typesetting and enable the typesetting of mathematical functions.
| > |
Representatives of the four classes are as follows
| > |
| > |
| > |
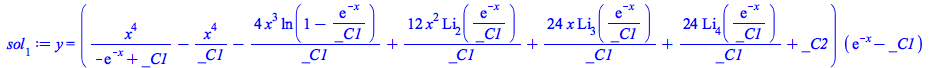 |
| > |
To verify that ode[1] does not admit point symmetries, construct the determining system and solve it
| > |
| > | (x, y))](DEs/DEs_14.png) |
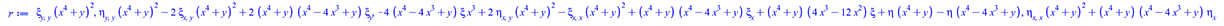 |
In this easy case, it suffices to run a differential elimination round to verify, without actually solving the PDE system, that in only admits trivial solutions, i.e. no point symmetries
| > | 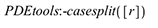 |
A representative of Non Point Symmetries Class II
| > |
| > |
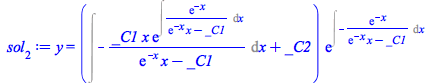 |
| > |
Representatives of the other classes
| > |
| > |
| > |
| > |
| > |
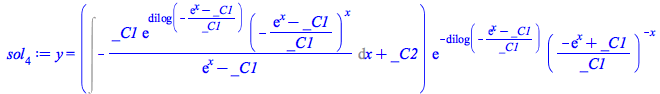 |
| > |
Previous Maple versions already include differential eliminations package, state-of-the-art, as DEtools[rifsimp] and DifferentialAlgebra, that use different methods to perform differential elimination, a key process towards decoupling a system of differential equations.
Maple 2018 adds a third elimination package, DifferentialThomas, which uses yet another method, in this way succeeding in triangularizing some nonlinear DE systems that cannot be handled in practical time by the previous two existing packages. Also, both DEtools[rifsimp] and DifferentialThomas when used through the PDEtools:-casesplit command admit a case time limit option. Combining different methods with a case-time-limit option is extremely useful in that branches of the splitting of nonlinear systems that cannot be handled in practical time by one package frequently can now be reconstructed and handled by the other one.
In addition, the new DifferentialThomas returns a disjoint decomposition of the given system, that is a decomposition where the solution of each case has no intersection with the solutions of the other cases (are not particular cases of the other other cases returned, as it may happen with the decompositions returned by DEtools[rifsimp] and DifferentialAlgebra)
Examples
| > |
This is one of Kamke's book 2nd order nonlinear examples, and is now decomposed into five disjoint cases - the general and four singular cases. This problem cannot be decomposed with DEtools[rifsimp] or DifferentialAlgebra.
When calling PDEtools:-casesplit, to indicate the use of the DifferentialThomas package, pass the package's name as additional argument (the same holds for RIF and DifferentialAlgebra)
| > |
| > |
One can also call directly the package commands with a list of differential equations as first argument and the ranking set by the package’s Ranking command
| > |
| > |